Schedule
Type | Day | Time | Place | Start | Lecturer |
V3 | Mo | 13:15-14:45 | AH IV | October 15 | |
Di | 10:00-11:30 | 5056 | October 16 | ||
Ü2 | Wed | 15:45-17:15 | AH VI | October 24 |
News
- 27.03.2013 A list carrying final grades for the second exam is uploaded.
- 26.03.2013 A list carrying student ids, points gained in the second exam and scheme for the grades is now online. The login is the same as for the solutions.
- 19.03.2013 The exam on the 22nd will take place at AH II and starts at 8:30 am. The revision of the exam is on the 27th from 3:00 P.M to 3:30 P.M in room 5052.
- 20.2.2013 The list with the points is now updated.
- 14.2.2013 The scheme for the grades is now available:
Mark | #Students | |||
>=47,5 | <=50 | 1 | 1 | 2,27% |
>=45 | <47,5 | 1,3 | 1 | 2,27% |
>=42,5 | <45 | 1,7 | 1 | 2,27% |
>=40 | <42,5 | 2 | 3 | 6,82% |
>=36,5 | <40 | 2,3 | 5 | 11,36% |
>=34 | <36,5 | 2,7 | 3 | 6,82% |
>=31,5 | <34 | 3 | 2 | 4,55% |
>=29 | <31,5 | 3,3 | 8 | 18,18% |
>=27,5 | <29 | 3,7 | 5 | 11,36% |
>=24,5 | <27,5 | 4 | 7 | 15,91% |
>=0 | <24,5 | 5 | 8 | 18,18% |
- The definition of nbp(v) has been adapted.
- Slide 36, point 4.2: it has been added that w is a final vertex.
- The second rule of slide 38 is applicable by taking an edge in G.
for local-choice CMSGs some problems arise.
Content and motivation
The Unified Modelling Language (UML) --- more generally, model-driven engineering --- plays an important role in modern software design. The UML basically consists of a set of different notations, each notation focused on a specific aspect of the software system at hand. The aim of this course is to consider some major fragments of the UML: sequence diagrams, hierachical state machines (also known as Statecharts), and the OCL (short for Object Constraint Language).
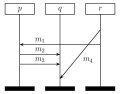 |
- Sequence diagrams specify the interaction patterns between the system components and are a popular elicitation technique for requirements engineering.
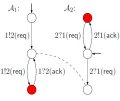 |
- Hierachical state machines and message passing automata are used to describe the behaviour of system components, and are intensively used during the system's design phases, e.g., in the fields of avionics and automotive industry.
- Finally, the OCL allows to specify properties of system components, ranging from pre- and postconditions to invariants and more complex properties.
Aims of this course
The aim of this course is to treat the theoretical underpinnings of the aforementioned UML fragments. In particular, we will present the theories required to:
- Clarify and make precise the semantics of the (treated fragments of the) UML;
- Reason about the basic properties of UML models;
- Algorithms to allow for the verification of such properties on UML models
It is our firm belief (and experience) that a solid theoretical underpinning is of prime importance to obtain automated tools (such as MSCan) that produce reliable, i.e, verifiable results.
Prerequisites
Although the name UML might suggest differently, this is a theoretical course! That is, a solid basis in algorithms and data structures, automata theory, and a bit of theoretical complexity theory is needed to be able to follow this course.
The course will cover for instance, formal semantics (how to precisly lay down the meaning of UML diagrams) and formal verification (is checking certain properties on UML diagrams decidable, and if so, efficiently decidable).
The course will cover for instance, formal semantics (how to precisly lay down the meaning of UML diagrams) and formal verification (is checking certain properties on UML diagrams decidable, and if so, efficiently decidable).
Basic knowledge of the undergraduate courses of the first two years (Vordiplom):
- Automata Theory
- Mathematical Logic
- Discrete Mathematics
- Complexity Theory
Further information
The course will be entirely given in English. The slides and other course material will also be in English. There are no lecture notes (yet); the course material will consist of slides. An examination will take place at the end of the course.
Slides and exercise sheets
Date | Lecture | Subject | Slides | |
15.10 | 1 | Introduction | ||
16.10 | 2 | Sequence Diagrams | ||
22.10 | 3 | Message Sequence Graphs | ||
29.10 | 4 | Properties of Message Sequence Graphs | ||
30.10 | 5 | Compositional Message Sequence Graphs | ||
5.11 | 6 | Communicating Finite State Machines | ||
Communicating Finite State Machines(slides) | ||||
19.11 | 7 | Languages and Subclasses of CFMs | ||
26.11 | 8 | Realisability | ||
27.11 | 9 | Safe Realisability | ||
4.12 | 10 | Regular MSCs | ||
10.12 | 11 | Realising Local Choice MSGs | ||
17.12 | 12 | A Logic for MSCs | ||
18.12 | 13 | Continue... | ||
7.1 | 14 | Continue... | ||
8.1 | 15 | Introduction to State-charts | ||
14.1 | 16 | Statechart Semantics (1) | ||
21.1 | 17 | Statechart Semantics (2) | ||
28.1 | 18 | Exam | ||
29.1 | Exam Solution |
Exercise | Exercise Sheet | Solutions | Due |
1 | 24.10 | ||
2 | 07.11 | ||
3 | 14.11 | ||
4 | 28.11 | ||
5 | 05.12 | ||
6 | 19.12 | ||
7 | 9.1 | ||
8 | 23.1 | ||
9 | 30.1 |
Additional background literature
Jos Warmer and Anneke Kleppe, Object Constraint Language, The: Precise Modeling with UML. Addison Wesley, 2001.
D. Harel and M. Politi, Modeling Reactive Systems with Statecharts: The STATEMATE Approach, McGraw-Hill, 1998.
Benedikt Bollig - Formal Models of Communicating Systems, Springer, 2006 (Chapter 7, 8 and 9)
(The course will however be mainly based on recent scientific papers.)

