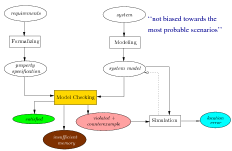The aim of this course is to present the basic principles of model checking, an automated verification technique for hard- and software systems. The starting point of model checking is a precise description of the possible system behaviors (typically given as a transition system), and the desired behaviour (typically a property expressed as logical formula). Model checking explores all possible system states in a brute force manner. In this way, it can be shown that all states in a given system model satisfy a certain property. In case of a property refutation, counterexamples are provided that act as diagnostic feedback and may be used to detect the cause of the violaton. Subtle errors that remain undiscovered using techniques such as simulation or peer reviewing can potentially be revealed using model checking. Model checking is thus an effective technique to expose potential design errors.

We start by introducing labeled transition systems and show that these are suitable for modeling sequential and concurrent programs. This is followed by a detailed study on various classes of system properties such as safety, liveness, and fairness. It will be shown how finite automata as well as variants thereof that accept infinite words are suitable for verifying regular properties. The linear-time and branching time temporal logics LTL and CTL are then introduced and compared. Model checking algorithms for these logics together with detailed complexity considerations  are covered. Finally, abstraction techniques based on bisimulation and simulation relations are covered.

modelling concurrent and communicating systems

• transition systems
• parallelism and communication
• the state-space explosion problem

linear time properties

• deadlocks
• reachability
• liveness
• fairness

regular properties

• automata on finite words
• automata on infinite words
• regular sequence properties

model checking

• linear time temporal logic (LTL)
• computation tree logic (CTL)

combating the state-space explosion

Sophisticated knowledge of the undergraduate courses of the first two years (Vordiplom):

• Automata Theory
• Mathematical Logic
• Discrete Mathematics
• Complexity Theory

Apart from these, no mandatory courses are required.

This lecture provides an introduction to a sequel of advanced courses:

The lecture and all material will be in English.